Linear Regression

Cost Function, MSE

“모델 성능 평가 지표”

cost function이 작다는 뜻은 실제값과 예측값의 차이가 적다는 뜻

즉, cost function 최소화 = 실제 데이터와 비슷하게 예측

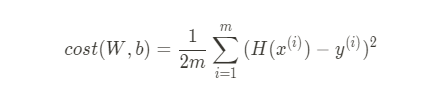
m이 아닌 2m으로 나눈 이유는 미분했을 때 내려오는 2와 나눠지게 하기 위함

Linear Regression

Liniear Regression 알고리즘은 학습데이터가 주어졌을 때, Cost값을 최소화 시켜주는 Hypothesis의 parameter(W,b)를 찾는 알고리즘

즉, MSE가 최소가 되도록 하는 직선을 찾는 것이 선형회귀분석이고 그 직선을 회귀선이라고 부르며 그 선의 함수를 회귀식이라고 부름

L1 regularization을 사용하는 regression model : Lasso Regression

L2 regularization을 사용하는 regression model : Ridge Regression

• Linear Regression은 L2 Loss를 사용하여 모델 fitting을 함

closed form

수학적 표현을 사용해서 정확하게 해를 표현할 수 있는 문제 ↔ open form

• 인풋데이터와 아웃풋데이터가 모두 1차원일 경우 closed form이 가능하므로 편미분하여 계산

file = open('경로','r')
tesxt = file.readlines()
file.close()

x_data = []
y_data = []

#convert to float
for s in text:
	data = s.split()
	x_data.append(float(data[0])
	y_data.append(float(data[1])

import numpy as np
#convert to numpy-array
x_data = np.asarray(x_data, dtype=np.float32)
y_data = np.asarray(y_data, dtype=np.float32)

import matplotlib.pyplot as plt
%matplotlib inline

plt.figure(1)
plt.plot(x_data, y_data, 'ro') # plot data
plt.xlabel('x-axis')  
plt.ylabel('y-axis')
plt.title('My data')

plt.show()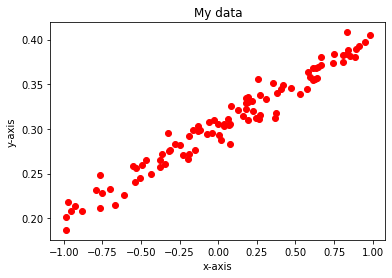

N = len(x_data) # the size of data
sum_of_x = np.sum(x_data)
sum_of_x_square = np.sum(x_data * x_data)
sum_of_y = np.sum(y_data)
sum_of_xy = np.sum(x_data * y_data)

a= (N * sum_of_xy - sum+of_x * sum_of_y) / (N * sum_of_x_square - sum_of_x ** 2)
b= (sum_of_y - a * sum_of_x) / N

plt.figure(2)

y_regression = a * x_data + b
plt.plot(x_data, y_data, 'ro')
plt.plot(x_data, y_regression, 'b')
plt.xlabel('x-axis')  
plt.ylabel('y-axis')
plt.title('Closed Form Regression')

plt.show()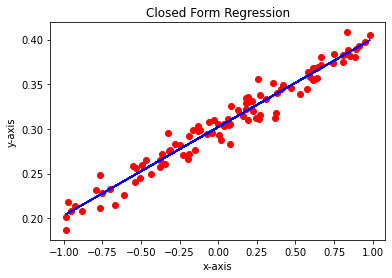

Gradient Descent 경사하강법

N차원일 경우 closed form solution이 존재하지 않을 수도 있고, 혹은 데이터가 너무 많거나 계산이 매우 복잡하여 정답을 구하기 힘든 경우 이용

 

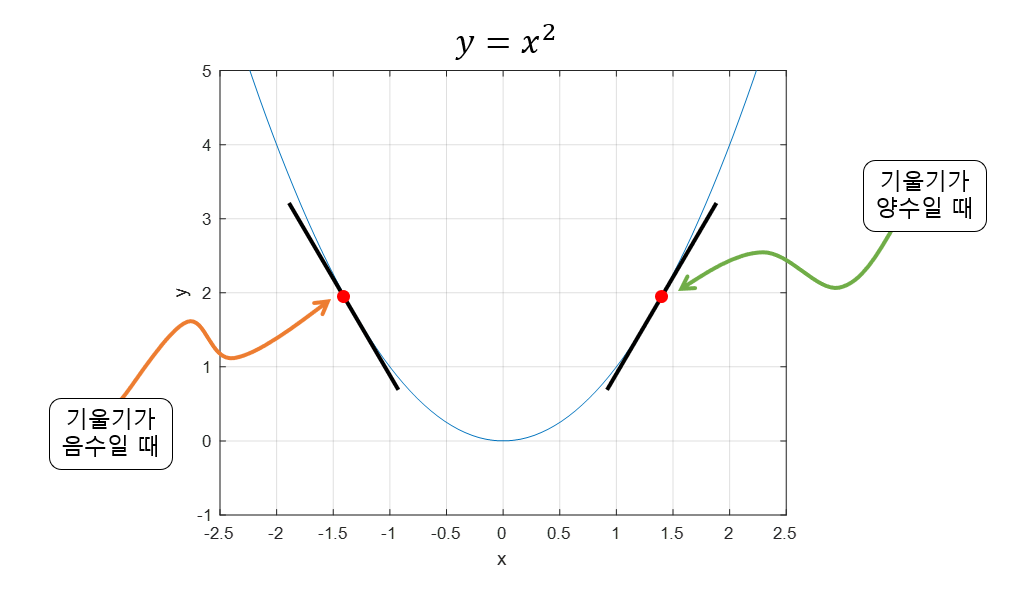
• 함수의 기울기를 이용해서 최소값 x를 찾기위한 방법

공식유도

기울기가 음수면 x를 양의 방향으로, 양수면 음의 방향으로 이동

 

• 이 식에서 기울기의 부호는 알 수 있지만 이동거리는 어떻게 구할까 ?

미분계수 (=기울기 =gradient)는 극소값에 가까워질수록 값이 작아짐

따라서, 이동거리는 미분계수와 비례

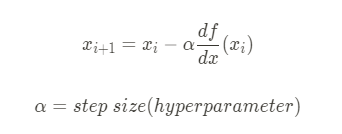
intercept 구하기

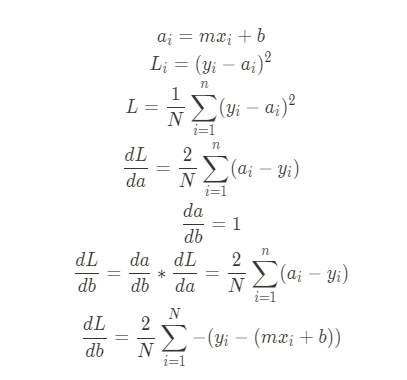
slope 구하기

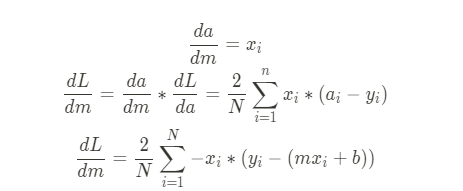
경사하강법의 문제점

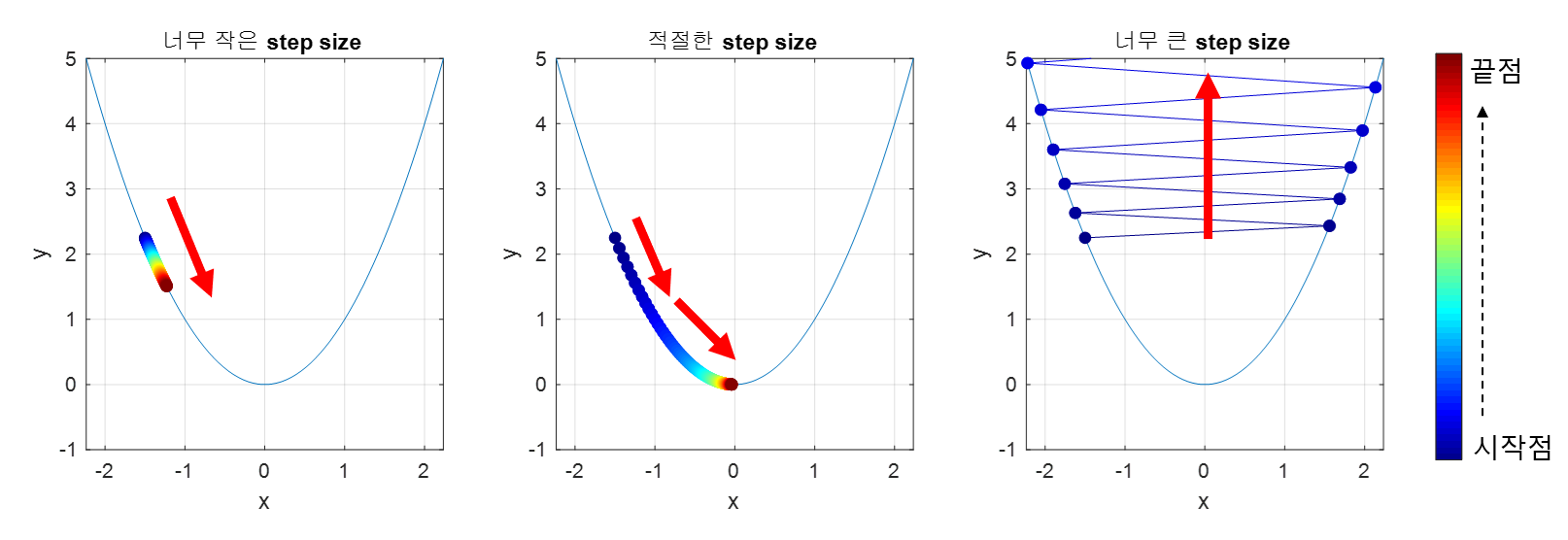
1. Step size (=$\alpha$)

적절한 step size 선택은 매우 중요

• step size가 큰 경우 이동 거리가 커지므로 빠르게 수렴할 수 있다는 장점이 있지만,
• 최소값으로 수렴되지 못하고 발산할 여지가 있음
• step size가 작은 경우 최소값을 찾는데 너무 오래 걸릴 여지가 있음

2. Local minima

우리가 찾고싶은건 global minima이지만, local minima에 빠져 벗어나지 못한 상황이 발생할 수 있음

하지만 최근에는 실제로 딥러닝이 수행될 때, local minima에 빠질 확률이 거의 없다고 함

실제 딥러닝 모델에서는 가중치(w)가 수도 없이 많고,

그 많은 w가 모두 local minima에 빠져야 업데이트가 정지됨

이론상 불가능에 가까우므로 사실상 local minima는 고려할 필요가 없다는 것이 중론

• python code로 직접 구현

# x:x-axis, y:y-axis, m:slope, b:intercept

def get_gradient_at_b(x,y,m,b):
	diff = sum([y_i - (m*x_i +b) for x_i,y_i in zip(x,y)])
	b_gradient = diff * (-2 / len(x))

	return b_gradient

def get_gradient_at_m(x, y, m, b):
  diff = sum([x_i * (y_i - (m * x_i + b)) for x_i, y_i in zip(x, y)])
  m_gradient = diff * (-2 / len(x))

  return m_gradient

# 계산된 gradient를 통해 b와 m 업데이트
def step_gradient(x,y,m_current,b_current,learning_rate):
	b_gradient = get_gradient_at_b(x, y, m_current, b_current)
  m_gradient = get_gradient_at_m(x, y, m_current, b_current)
  b = b_current - (learning_rate * b_gradient)
  m = m_current - (learning_rate * m_gradient)

  return [b, m]

from matplotlib import pyplot as plt

months = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
revenue = [52, 74, 79, 95, 115, 110, 129, 126, 147, 146, 156, 184]

# b와 m을 0으로 초기화합니다
b1, m1 = 0, 0
y1 = [m1 * month + b1 for month in months]
plt.plot(months, y1)
# learning_rate를 0.001로 설정한 후 한 step 나아갑니다
b2, m2 = step_gradient(months, revenue, b1, m1, 0.001)
y2 = [m2 * month + b2 for month in months]
plt.plot(months, y2)

plt.show()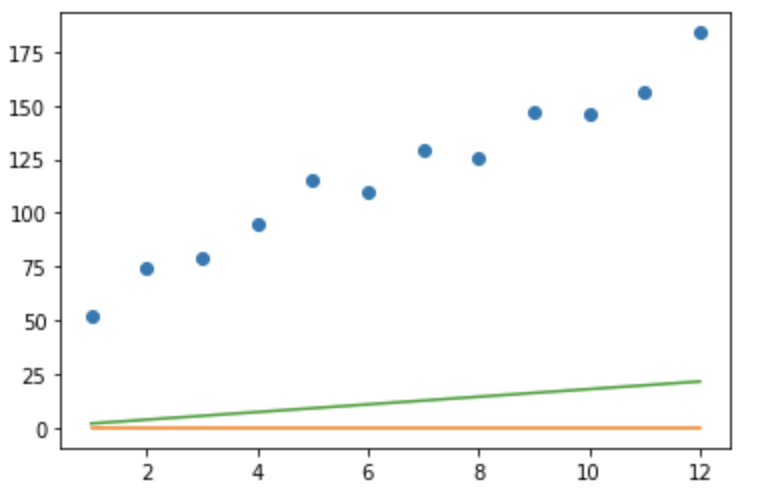

초록색 직선이 살짝 위로 올라갔음

몇 step을 더 거쳐야 할지 어떻게 알까 ?

convergence

파라미터가 변하더라도 loss가 더이상 잘 변화하지 않는 텀

파라미터를 m과 b를 언제까지 변화시켜야 할 지 알기 위해선 convergence를 알아야 함

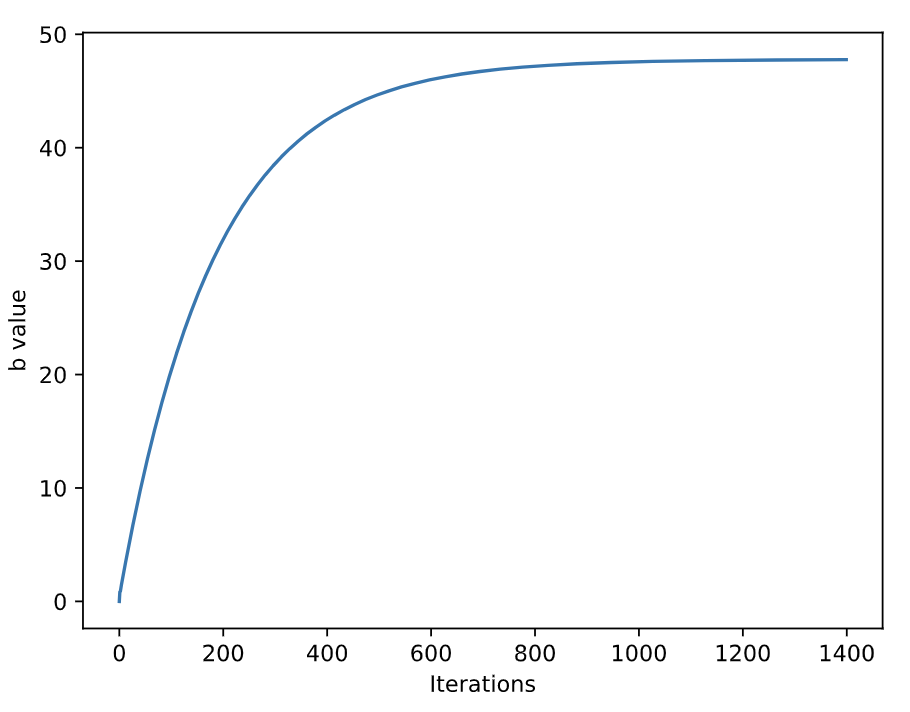
그래프에서 약 800 iteration부터 변화가 없는데, 이 시기가 바로 convergence다

learning rate

learning rate는 한 step에서 gradient가 변화하는 양

데이터를 가장 잘 나타내는 직선을 나타내기 위해선 m과 b를 loss가 감소하는 방향으로 나아가게 해야한다고 앞서 설명했다.

그럼 얼마나 나아가야 적절할까

너무 작은 learning rate는 converage까지 많은 시간이 걸리고,

너무 큰 learning rate는 가장 작은 loss값을 지나칠 수 있다 (발산)

def gradient_descent(x, y, learning_rate, num_iterations):
  m, b = 0, 0	# 0으로 초기화
  for i in range(num_iterations):
    # num_iterations 만큼 step을 진행합니다
    b, m = step_gradient(b, m, x, y, learning_rate)

  return [b, m]

b, m = gradient_descent(months, revenue, 0.01, 1000)
y = [m*x + b for x in months]

plt.plot(months, revenue, "o")
plt.plot(months, y)
plt.show()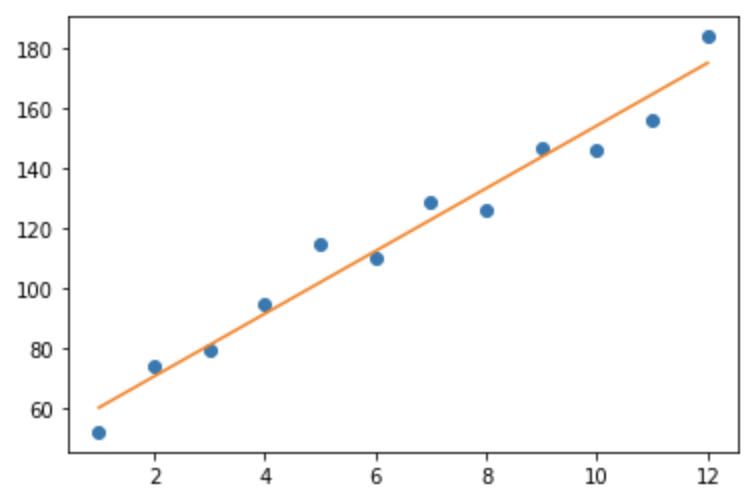

• torch로 구현

import torch
import torch.nn as nn

# Hyper-parameters
input_size = 1
output_size = 1
num_epochs = 100
learning_rate = 0.1

# Linear regression model, y = Wx+b
model = nn.Linear(input_size, output_size)

# Loss and optimizer
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

#numpy와 다르게 pytorch는 두번째 shape에 차원이 들어가줘야함
print(x_data.shape, y_data.shape)
>> (100,)(100,)
if len(x_data.shape)==1 and len(y_data.shape)==1:
  x_data = np.expand_dims(x_data, axis=-1)
  y_data = np.expand_dims(y_data, axis=-1)
print(x_data.shape, y_data.shape)
>> (100,1)(100,1)

# Train the model
for epoch in range(num_epochs):
    # Convert numpy arrays to torch tensors
    inputs = torch.from_numpy(x_data)
    targets = torch.from_numpy(y_data)

    # Predict outputs with the linear model.
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    
    # compute gradients and update
    optimizer.zero_grad() #옵티마이저 미분값 초기화
    loss.backward() #미분 계산
    optimizer.step() #업데이트
    
    if (epoch+1) % 5 == 0:
        print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))

Epoch [5/100], Loss: 0.1971

Epoch [10/100], Loss: 0.0260

Epoch [15/100], Loss: 0.0057

Epoch [20/100], Loss: 0.0023

Epoch [25/100], Loss: 0.0013

Epoch [30/100], Loss: 0.0008

Epoch [35/100], Loss: 0.0005

Epoch [40/100], Loss: 0.0003

Epoch [45/100], Loss: 0.0002

Epoch [50/100], Loss: 0.0002

Epoch [55/100], Loss: 0.0002

Epoch [60/100], Loss: 0.0001

Epoch [65/100], Loss: 0.0001

Epoch [70/100], Loss: 0.0001

Epoch [75/100], Loss: 0.0001

Epoch [80/100], Loss: 0.0001

Epoch [85/100], Loss: 0.0001

Epoch [90/100], Loss: 0.0001

Epoch [95/100], Loss: 0.0001

Epoch [100/100], Loss: 0.0001

# Plot the graph
predicted = model(torch.from_numpy(x_data)).detach().numpy()
plt.plot(x_data, y_data, 'ro', label='Original data')
plt.plot(x_data, predicted, label='Fitted line')
plt.legend()

plt.show()